Méthodologie

Comme cet article contient des équations mathématiques, j’ai utilisé l’outil LaTeX pour la rédiger. J’ai ensuite généré mon article au format PDF grâce à l’outil latexmk. Je vous en dit plus sur mon article d’introduction à LaTeX.

Si vous le souhaitez, téléchargez les sources LaTeX de l’article : bases-proba.tex.

J’ai également rédigé un transcript de l’article, ci-dessous, mis ici à des fins de référencement.
Je vous conseille de lire la version PDF; cette version textuelle est moins adaptée à la lecture.

J’ai utilisé Cloud Convert pour transformer l’article en Markdown, que j’ai modifié manuellement pour qu’il soit plus lisible, et enfin passé dans https://upmath.me pour convertir les formules en images SVG avec à nouveau quelques modifications manuelles.

Si c’était à refaire, je passerais directement par Upmath.me. Il me faudrait ensuite une solution automatisée pour récupérer toutes les images SVG : à l’heure actuelle, si le site upmath.me disparaît, mes formules aussi. Peut-être que cloner https://github.com/parpalak/i.upmath.me est une bonne solution : héberger une version du site sur un serveur que je gère moi-même.

Lire cet article au format PDF (beaucoup plus lisible)

Transcript

Union et intersection

Intersection entre A et B (A inter B) :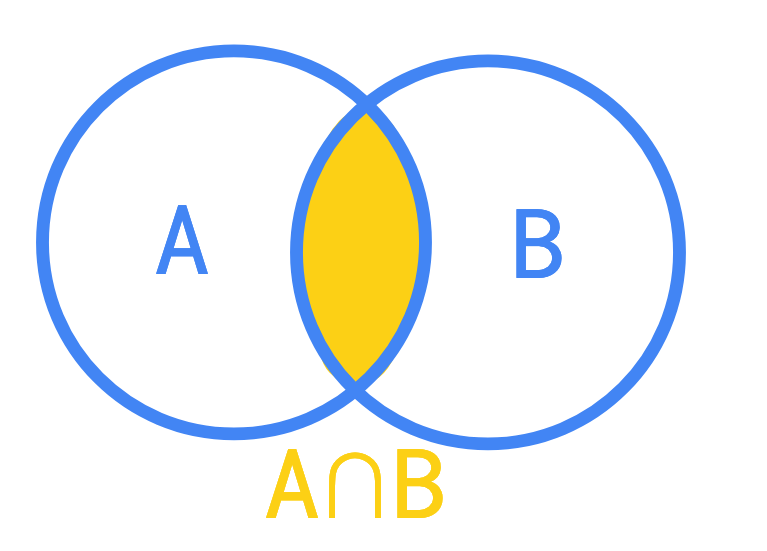
Intersection A inter B

Union entre A et B (A union B), entre C et D (C union D) :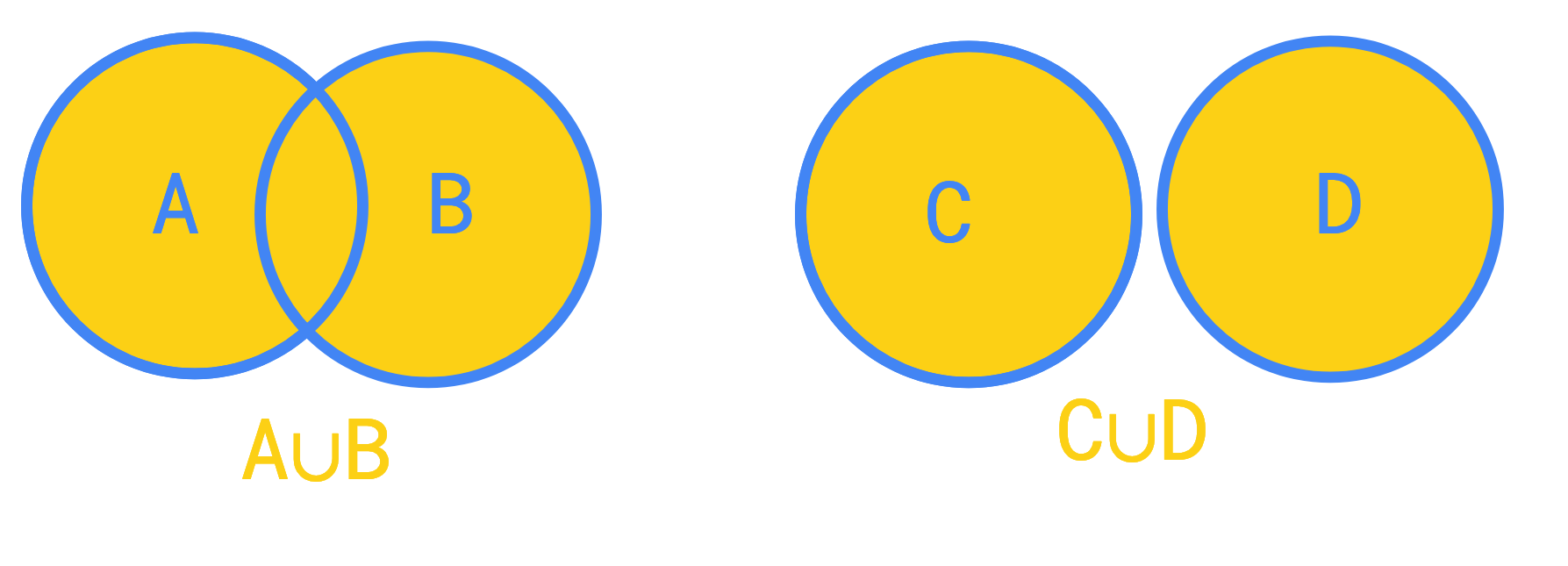
Union A U B et C U D

Propriétés

$0 \leq P(A) \leq 1$
$P(\overline{A}) = 1 - P(A)$
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
$P(A \cap B) = P(A) * P(B)$ si A et B sont indépendants
$P(\overline{A} \cup \overline{B}) = P(\overline{A \cap B}) = 1 - P(A \cap B)$
$P(\overline{A} \cap \overline{B}) = P(\overline{A \cup B}) = 1 - P(A \cup B)$

Calcul d’une probabilité

Formules

Pour calculer une probabilité, on calcule le nombre de combinaisons possibles de l’évenement recherché Card(A) , qu’on divise par le nombre total de combinaisons possibles $Card(\Omega)$ : $\frac{Card(A)}{Card(\Omega)}$ . On appelle ce nombre de combinaisons “cardinal”.

Pour calculer un cardinal, il existe 3 formules à appliquer selon la situation :

Situation	Formule	Calcul
Simultané	$C_{n}^{p}$	$\frac{n!}{p!(n-p)!}$
Successif sans remise	$A_{n}^{p}$
Successif avec remise

Exemples de calculs utilisant ces formules :

$C_{3}^{7} = \frac{7!}{3!4!} = \frac{7*6*5*4!}{3!*4!} = \frac{35 * 3 * 2}{3 * 2} = 35$

$A_{3}^{7} = 7 * 6 * 5 = 7 * 30 = 210$

$3^{7} = 3333333 = 2187$

Exemples

Nous avons 3 abricots et 4 pommes.

Tirage successif avec remise

Quelle est la probabilité de tirer successivement 5 abricots, en les remettant en place après chaque tirage ?

Nous tirons 5 fois, et 3 des éléments sont des abricots. Le cardinal de notre évenement est $Card(A) = 3^{5} = 243$

Nous avons un total de 8 éléments sur chacun des tirages. Calculons le cardinal : $Card(\Omega) = 7^{5} = 16807$

Nous avons ainsi $\frac{Card(A)}{Card(\Omega)} = \frac{243}{16807} \approx 1,45\%$ de tirer 5 abricots d’affilée.

Même calcul, mais cette fois pour tirer 3 abricots suivis de 2 pommes : $\frac{Card(A)}{Card(\Omega)} = \frac{3^{3} * 4^{2}}{7^{5}} = \frac{432}{16807} \approx 2,57\%$

Cette notation peut être comprise de la manière suivante : nous avons $\frac{3}{7}$ de tirer un abricot, puis à nouveau $\frac{3}{7}$ deux autres fois. Nous avons ensuite (https://i.upmath.me/svg/%5Cfrac%7B4%7D%7B7%7D" alt=”\frac{4}{7}” /> de tirer une pomme, deux fois de suite. Nous pouvons ainsi écrire notre probabilité sous la forme $\frac{3}{7} * \frac{3}{7} * \frac{3}{7} * \frac{4}{7} * \frac{4}{7}$ , qui correspondent bien à notre notation $\frac{3^{3} * 4^{2}}{7^{5}}$ .

Tirage successif sans remise

Quelle est la probabilité de tirer successivement 1 abricot puis 1 pomme, sans les remettre en place après chaque tirage ?

deux_abricots_puis_trois_pommes

Commençons par le tirage des abricots. Nous avons 3 abricots disponibles, et nous voulons en tirer deux d’affilée. Nous avons 7 fruits au début du tirage. $\frac{Card(A)}{Card(\Omega)} =\frac{A_{2}^{3}}{A_{2}^{7}} = \frac{\cancel{3*2}}{7*\cancel{6}} =\frac{1}{7} \approx 14\%$ . Nous avons ainsi environ 14% de probabilité de tirer deux abricots de suite.

Continuons avec les pommes. Notre univers (https://i.upmath.me/svg/%5COmega" alt=”\Omega” /> n’est désormais plus constitué que d’1 abricot et 4 pommes, soit un total de 5 fruits. Nous voulons tirer 3 des 4 pommes, d’affilée. $\frac{Card(A)}{Card(\Omega)} =\frac{A_{3}^{4}}{A_{3}^{5}} =\frac{\cancel{4}*\cancel{3}*2}{5*\cancel{4}*\cancel{3}} =\frac{2}{5} = 40\%$ de probabilité de tirer 3 pommes d’affilée, sur les 5 fruits disponibles.

En mettant bout à bout nos deux probabilités successives, nous avons $\frac{1}{7} * \frac{2}{5} = \frac{2}{35} \approx 5,71\%$ de probabilité que notre évenement complet, le tirage de 2 abricots puis de 3 pommes, se produise.

Nous pouvons reproduire ce calcul en calculant évenement après évenement: $\frac{3}{7} * \frac{2}{6} * \frac{4}{5} * \frac{3}{4} * \frac{2}{3}$ , ce qui correspond bien à notre calcul.

Tirage simultané

Quelle est la probabilité de tirer simultanément 2 abricots et 1 pomme ?

tirage souhaité

Nous devons trouver 2 abricots sur 3 disponibles Card(A) = C_3^2 et 1 pomme sur 4 disponibles Card(A) = C_1^4 . Calculons le cardinal de notre évenement : $Card(A) . Card(B) = C_3^2 . C_1^4 = \frac{\cancel{3!}}{2!1!} * \frac{4!}{1!\cancel{3!}} = \frac{43\cancel{2!}}{\cancel{2!}} = 12$

Le cardinal de l’univers, soit toutes les possibilités, correspond à 3 fruits tirés sur 7 disponibles : $Card(\Omega) = C_7^3 = \frac{7!}{3!4!} = \frac{765\cancel{4!}}{32\cancel{4!}} = \frac{7*\cancel{6}*5}{\cancel{6}} = 35$

Nous avons donc $\frac{Card(A) . Card(B)}{Card(\Omega)} = \frac{12}{35} \approx 0.34$ environ 34% de chances que cet évenement se produise.

Sauvajon.tech

Les bases de calcul des probabilités